VEPFIT is an analysis software for depth-profiling doppler broadening positron annihilation measurements for slow positron beams. The main analysis includes analysis defect parameters \(S\) and positronium fraction \(F\).
For the transport of mono-energetic positrons in defect free solids, the implantation profile can be parameterized by the Makhovian distribution.
\[P(z) = \frac{m z^{m-1}}{z_{0}^{m}} e^{-\frac{z}{z_{0}}^m}\]The standard values and units of the Makhovian profile are discussed in the positron annihilation link.
At a depth \(z\), the time averaged positron density \(c(z)\) below the solid surface is given by a second order diffusion differential equation,
\[D^{+} \frac{d^{2} c}{dz^{2}} - \frac{d}{dz} (v_{d} c) + I(z) - \kappa_{t} n_{t} c - \lambda_{b} c = 0\]where \(c=c(z)\) is the time averaged positron density and \(v_{d}(z)\) is the drift velocity, which can also be written in terms of electric field, \(\mu E(z)\). \(I(z)\) is the positron stopping rate as a function of depth, with units of density increase/second. \(n_{t}(z)\) is the defect density. \(\kappa_{t}\) is the rate constant for positrons trapping at defects and \(\lambda_{b}\) is the bulk annihilation rate. Lastly, \(D^{+}\) is the positron difussion constant.
Both the stopping profile \(p(z*)\) and the positron density \(c(z)\) can be generalized by introducing a normalization term, integrating over the positron stopping rate \(I(z)\),
\[I_{norm} = \int_{0}^{\infty} I(z^{*}) dz*\]Rewriting \(p(z)\) and \(c(z)\) in normalized form,
\[p(z^{*}) = \frac{I(z^{*})}{I_{norm}}\] \[c^{*}(z^{*}) = \frac{D^{+} c(z^{*})}{a^{2} I_{norm}}\]Furthermore, this introduces generalized terms for depth and drift velocity:
\[z^{*} = \frac{z}{a}\]where a is the lattice parameter
\[v_{d^{*}} = (v_{d} a / D^{+})\] \[\mu = e D^{+}/kT\]The new positron density equation can be written in terms of generalized parameters as
\[\frac{d^{2} c^{*}}{dz^{*2}} - \frac{d}{dz^{*}} (v_{d}^{*} c^{*}) + p(z^{*}) - \frac{a^{2}}{D^{+}} (\kappa_{t} n_{t} + \lambda_{b}) c^{*} = 0\]integrating the differential equation yields,
\[\bigg( \big( \frac{dc*}{dz*} \big)_{z*=0} - v_{d^{*}}(0) c^{*}(0) \bigg) + 1 - \bigg( \int_{0}^{\infty} \big( \frac{a^{2}}{D^{+}} (\kappa_{t} n_{t} + \lambda_{b}) \big) c^{*} dz^{*} \bigg) = 0\]these terms can be reduced to define the fraction of stopped positrons. For surface transmitted positrons,
\[-F_{s} = \big( \frac{dc^{*}}{dz^{*}} \big)_{z^{*}=0} - v_{d^{*}}(0) c^{*}(0)\]for the fraction of positrons trapped in defects
\[F_{t} = \int_{0}^{\infty} \frac{a^{2}}{D^{+}} \kappa_{t} n_{t} c^{*} dz^{*}\]and the fraction of positrons annihilated in the bulk
\[F_{b} = \int_{0}^{\infty} \frac{a^{2}}{D^{+}} \lambda_{b} c^{*} dz^{*}\]In principle, for large depths \(z \rightarrow \infty\), positron concentration becomes negligible and satifies \(c(z\rightarrow \infty) = 0\).
In practice, it may be more useful to define a depth \(z_f\) where no positrons are stopped and no defects are present. The solution to the differential equation introduces the positron diffusion length, \(L_{+}\), assuming a uniform defect density,
\[c(z) = c(z_{f}) e^{-a (z - z_{f}) / L_{+}}\]The diffusion length in a pure material is defined as,
\[L_{+} = (\frac{D^{+}}{\lambda_{b}})^{1/2}\]If we set the boundary condition \(z=z_{f}\), then,
\(\big(\frac{dc}{dz}\big)_{z=z_f} = -c(z_{f}) / L_{+}\),
the diffusion length then becomes the effective diffusion length, \(L_{+,eff}\),
\[L_{+,eff} = \big[ D^{+} / (\kappa_{t} n_{t} + \lambda_b) \big]^{1/2}\]An absorption length, \(L_{a}\) can also be defined if the boundary condition \(z=0\) is chosen,
\[\big( \frac{dc}{dz} \big) = c(z=0)/ L_{a}\]For the case of \(E(z) = 0\), The general solution the differential equation with generalized parameters (asteriks indicating that they are generalized have been omitted) is,
\[c(z) = A e^{\gamma z} + B e^{-\gamma z} + p/\alpha\]where \(\gamma^{*,-} = 1/2 [-v_{d} \pm (v^{2}_{d} + 4 \gamma^{2})^{1/2}]\). The terms \(p(z)\), \(n_{t}(z)\) and \(E(z)\) assuming that they are slowly varying over \([z,z+\Delta z]\) and can be taken as constants
Data file formats should include the following columns:
| Energy (keV), Doppler Parameters (S or W), Positronium Fraction, \(\Delta S\), \(\Delta F_{ps}\) |
The data analysis software (VEPFIT) can only run on Windows 98 for now. Rather than installing the ancient OS on your drive, we get around this through Virtual Box.
VirtualBox’s guest additions add on is not supported in Windows 98, the browsers on W98 are not functional, and I haven’t figured out how to transfer files via network. So creating a vhd seems to be the most hassle free way to do this.
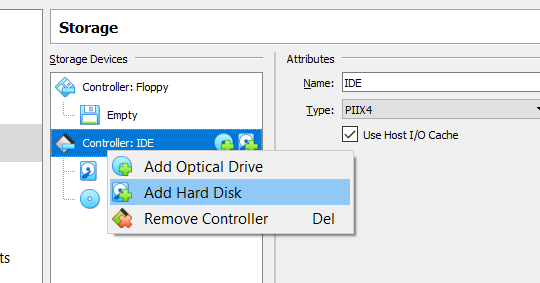
1) In VirtualBox, create a new virtual hard disk (vhd), don’t make it too large, I found that 100mb works.

2) In the Windows 98 VM, open up the MS-DOS prompt and type fdisk.
2.5) If you are asked to enable large disk support, just enter yes.
3) Select option 5 in the “Change current fixed disk drive”.
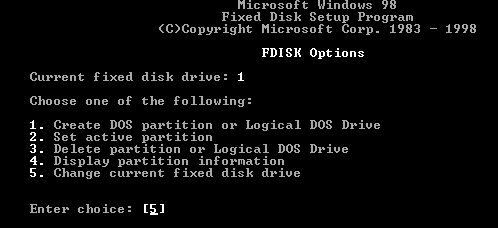
4) You will be prompted to “Enter a fixed drive number”. The vhd will not display exactly 100mb (maybe 91mb). Hit enter.
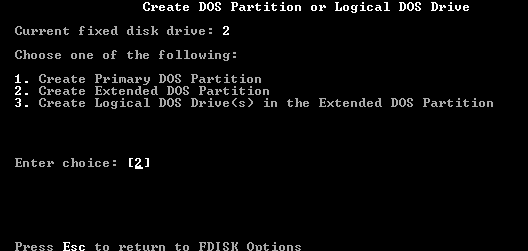
5) With the vhd selected, create an extended DOS partition (option 2).
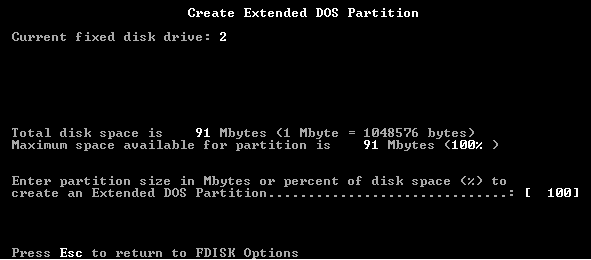
6) When you get to the screen below, just verify that the maximum space to allocate is 100%. Hit enter.
7) The file explorer in Windows 98 should display a “D:” drive now (if you don’t see this, restart the VM). However, you need to format this D: drive in order to use it.
8) Open up the MS-DOS prompt again and type format d:
9) Copy any files or data you need to transfer into the D: drive and MAKE SURE YOU SHUT THE VM OFF BEFORE TRANSFERING.
10) Locate the .vhd (usually in the same folder as the Win98 .vhd, or where ever you specified in step 1). You can view the contents and extract them using 7zip.
[1] Analysis of positron profiling data by means of ‘‘VEPFIT’’